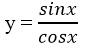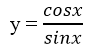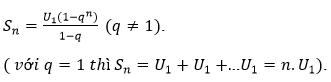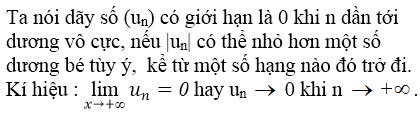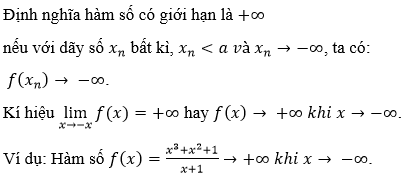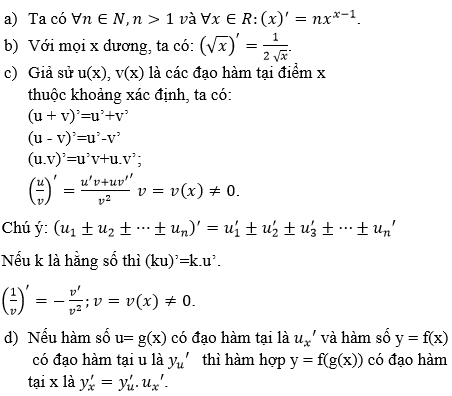Bài 1 (trang 178 SGK Đại số 11): Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và tập giá trị của từng hàm số đó.
Lời giải:
a. Định nghĩa 1 : (Hàm số sin): Quy tắc tương ứng với mỗi số thực x với số thực sinx.
sin: R -> R
x -> y = sinx.
Hàm số y = sinx có tập xác định là R, tập giá trị là đoạn [-1;1].
b.Định nghĩa 2 : (Hàm số cosin): Quy tắc tương ứng với mỗi số thực x với số thực cosx.
cos : R -> R
x -> y = cosx.
Hàm số y = cosx có tập xác định là R, tập giá trị là đoạn [-1;1]
c. Định nghĩa 3: (Hàm số tang): Hàm số tang là hàm số được xác định bởi công thức
tan : D -> R
x -> y = tanx.
Hàm số y = tanx có tập xác định
Tập giá trị của hàm số y = tanx là R.
d. Định nghĩa 4 : (Hàm số cotang): là hàm số được xác định bởi công thức
cot : D -> R
x -> y = cotx.
Hàm số y = cotx có tập xác định D = {x ∈ R x ≠ kπ, k ∈ Z}. Tập giá trị của hàm số y = coty là tập R.
Bài 2 (trang 178 SGK Đại số 11): Cho biết chu kì của mỗi hàm số y = sinx, y = cosx, y = tanx, y = cotx.
Lời giải:
a. Hàm số y = sinx và y = cosx là hàm số tuần hoàn có chu kì là 2 π.
b. Hàm số y = tanx và y = cotx là các hàm số tuần hoàn có chu kì là π.
Bài 3 (trang 178 SGK Đại số 11): Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình asinx + bcosx = c.
Lời giải:
Bài 4 (trang 178 SGK Đại số 11): Viết công thức tính số hoán vị của tập hợp gồm n phần tử (n > 1). Nêu ví dụ.
Lời giải:
Kí hiệu Pn là các số hoán vị của tập hợp gồm phần tử (n > 1) và Pn được xác định: Pn=1.2….n hay Pn=n!
Ví dụ: Tính số các hoán vị của tập A = {a, b, c, d}.
Giải
Tập A có 4 phần tử, do đó số hoán vị của tập A là P4=24.
Bài 5 (trang 178 SGK Đại số 11): Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
Lời giải:
Ví dụ: Một lớp học gồm 50 học sinh. Cần lập một đoàn đại biểu đi dự đại hội đoàn trường gồm 3 học sinh. Hỏi có bao nhiêu cách lập.
Giải: Rõ ràng một nhóm 3 học sinh chính là một tổ hợp chập 3 của 50. Do đó số cách lập đoàn đại biểu là : C503=19600 (cách).
Bài 6 (trang 178 SGK Đại số 11): Viết công thức nhị thức Niutơn.
Lời giải:
Công thức nhị thức Niutơn:
(a+b)n = Cn0 an + Cn1an-1 b + Cn1an-2 b2 + … + Cnn-1a bn-1 + Cnn bn.
Chú ý: số hạng T(k+1) =Cnk a(n-k)bk được gọi là số hạng tổng quát của khái triển (a+b)n.
Bài 7 (trang 178 SGK Đại số 11): Phát biểu định nghĩa xác suất của biến cố.
Lời giải:
Giả sử A là một biến cố liên quan đến một phép thử với không gian mẫu Ω chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Kí hiệu n(Ω), n(A) theo thứ tự là số các kết quả có thể xảy ra của phép thử và số phần tử của A. Ta gọi là xác suất của biến cố A, kí hiệu P(A) là tỉ số sau:
Bài 8 (trang 178 SGK Đại số 11): Nêu rõ các bước chứng minh bằng quy nạp toán học và cho ví dụ
Lời giải:
Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈N ∗ là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:
Bước 1: Kiểm tra mệnh đề đúng với n =1 .
Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.
Bước 3: Kết luận mệnh đề đúng với n ∈N ∗.
Ví dụ: Chứng minh rằng với mọi n ∈N ∗ ta có:n3+5n chia hết cho 6.
Chứng minh: Đặt P(n) = n3+5n.
Với n =1 => P(1) = 6 ⋮ 6
Giả sử (Pn) chia hết cho 6 đúng với n=k ≥1, nghĩa là, ta có:
P(k)=(k3+5k)⋮6.
Ta có: P(k+1)=(k+1)3+5(k+1)=k3+3k2+3k+1+5k+5
=k3+5k+3(k2+k)+6
Mặt khác, theo giả thiết quy nạp ta có: k3+5k)⋮6.
Hơn nữa k2+k=k(k+1):2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).
Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.
Theo nguyên lí quy nạp, ta có P(n) = n3+5n chia hết cho 6 với mọi n ∈N ∗.
Bài 9 (trang 178 SGK Đại số 11): Phát biểu định nghĩa cấp số cộng và công thức tính tổng n số hạng đầu tiên của một số không đổi d.
Lời giải:
Định nghĩa: cấp số cộng là một dãy số ( hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
Ta có: U(n+1) =Un+d , ∀n ∈N ∗
Cho cấp số cộng (Un) công sai d. đặt Sn=U1+U2+..+Un
Khi đó:
Bài 10 (trang 178 SGK Đại số 11): Phát biểu định nghĩa cấp số nhân và công thức tổng n số hạng đầu tiên của một cập số nhân.
Lời giải:
Định nghĩa: Cấp số nhân là một dãy số ( hữu hạn hoặc vô hạn), trong đó từ số hạng thứ hai; mỗi số hạng đều là tích các số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Ta có: U(n+1)=Un.q,∀n ∈N ∗.
Cho cấp số nhân (Un ),công bội q. đặt Sn=U1+U2+..+Un
Khi đó:
Bài 11 (trang 178 SGK Đại số 11): Dãy số Un thỏa mãn điều kiện gì thì được gọi là có giới hạn 0 khi n dần tới dương vô cực?
Lời giải:
Bài 12 (trang 178 SGK Đại số 11): Viết công thức tính tổng của một cấp số nhân lùi vô hạn.
Lời giải:
Bài 13 (trang 178 SGK Đại số 11): Định nghĩa hàm số có giới hạn + ∞ khi x -> – ∞
Lời giải:
Bài 14 (trang 178 SGK Đại số 11): Nêu các giới hạn đặc biệt của dãy số.
Lời giải:
Bài 15 (trang 178 SGK Đại số 11): Nêu định nghĩa hàm liên túc tại một điểm, trên một khoảng. Nêu nhận xét về đồ thị của một hàm số liên tục trên một khoảng.
Lời giải:
+ Hàm số liên tục tại một điểm
+ Hàm số liên tục trên một khoảng
– Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
– Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
Bài 16 (trang 178 SGK Đại số 11): Phát biểu định nghĩa đạo hàm của hàm số y=f(x)tại x=xo.
Lời giải:
Bài 17 (trang 178 SGK Đại số 11): Viết tất cả các quy tắc tính đạo hàm đã học
Lời giải:
Bài 18 (trang 178 SGK Đại số 11): Giả sử hàm số y = f(x) có đạo hàm tại xo. Hãy viết phương trình tiếp tuyến của đồ thị hàm số g = f(x) có đạo hàm tại x