Bài 1 (trang 46 SGK Đại số 11): Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:
a.Một chữ số
b.Hai chữ số.
c.Hai chữ số kháu nhau?
Lời giải:
a.Đặt A = {1, 2, 3, 4}
+ Gọi số có 1 chữ số là a
+ a có 4 cách chọn.
Vậy có 4 cách chọn số một chữ số.
b. Gọi số có 2 chữ số là ab
+ a có 4 cách chọn
+ b có 4 cách chọn
Vậy theo quy tắc nhân ta có: 4.4 = 16 (số)
c. Một số tự nhiên có hai chữ số khác nhau lập từ 4 chữ số trên có thể lập bằng cách chọn chữ số hàng chục: 4 cách.
Sau khi chọn chữ số hàng chục thì còn 3 cách chọn chữ số hàng đơn vị.
Vậy có 4.3 = 12 số tự nhiên có hai chữ số khác nhau được lập từ 4 chữ số trên.
Bài 2 (trang 46 SGK Đại số 11): Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
Lời giải:
Đặt B = {1, 2, 3, 4, 5, 6}
+ Gọi số tự nhiên bé hơn 100 là a và cd
+ Số cách chọn chữ số a là 6 cách
+ Số cách chọn chữ số c là 6 cách
+ Số cách chọn chữ số d là 6 cách
+ Số cách chọn chữ số cd là 6.6 = 36 cách.
Theo quy tắc cộng thì số cách chọn thỏa yêu cầu bài toán là:
6 + 36 = 42 (số)
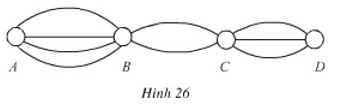
Bài 3 (trang 46 SGK Đại số 11): Dưới thành phố A, B, C, D được nối với nhau bởi các con đường như hình dưới:
Hỏi:
a. Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
b. Có bao nhiêu cách đi từ A đến D rồi quay lại A?
Lời giải:
a.+Từ A đến B có 4 con đường nên có 4 cách đi
+ Từ B đến C có 2 con đường nên có 2 cách đi.
Vậy từ A đến C có 4.2 = 8 cách đi.
+Từ C đến D có 3 con đường nên có 3 cách đi
Vậy từ A đến D có 8.3 = 24 cách đi.
b.Theo câu a thì từ A đến D có 24 cách đi nên từ D đến A cũng có 24 cách đi. Vậy số cách đi từ A đến D rồi trở về A là 24.24 = 576 (cách đi)
Bài 4 (trang 46 SGK Đại số 11): Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
Lời giải:
– Có 3 kiểu mặt đồng hồ nên có 3 cách chọn.
– Có 4 kiểu dây nên có 4 cách chọn.
Vậy số cách chọn một chiếc đồng hồ gồm một mặt và một dây là:
3.4 = 12 cách