Bài 1 (trang 40 SGK Đại số 11):
a.Hàm số y = cos3x có phải là hàm số chẵn không?Tại sao?
b.Hàm số y = tan(x+ π/5) có phải là hàm số lẻ không?Tại sao?
Lời giải:
a.y= f(x) = cos3x là hàm số chẵn vì:
TXĐ: D = R
∀x∈ D ta có: – x ∈ D
Xét: f(-x) = cos(-3x) = cos3x = f(x)∀ x∈ D
Bài 2 (trang 40 SGK Đại số 11): Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn[-3π/2 ; 2π] để hàm số đó:
a. Nhận giá trị bằng – 1
b. Nhận giá trị âm
Lời giải:
Đồ thị hàm số y = sinx:
a.Dựa vào đồ thị hàm số, ta thấy trên đoạn [-3π/2 ; 2π] , để hàm số y = sinx nhận giá trị bằng -1 thì
b.Đồ thị hàm số y = sinx nhận giá trị âm trên đoạn [-3π/2 ; 2π] trong các khoảng ( – π, 0) và (π, 2π)
Bài 3 (trang 41 SGK Đại số 11): Tìm giá trị lớn nhất của các hàm số sau:
Lời giải:
Ta có: cosx ≤ 1
=>1 + cos x ≤ 2 <=> 2(1+cos x) ≤ 4
Bài 4 (trang 41 SGK Đại số 11): Giải phương trình sau:
Lời giải:
Bài 5 (trang 41 SGK Đại số 11): Giải các phương trình sau:
a. 2cos2x – 3cosx + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
c. 2sinx + cosx = 1
d. sinx + 1,5cotx = 0
Lời giải:
a. 2cos2x – 3cosx + 1 = 0 (1)
Đặt t = cosx với điều kiện – 1 ≤ t ≤ 1
(1) 2t2 – 3t + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
<=> 25sin2x + 15.2sinx.cosx + 9cos2x = 25(sin2x + cos2x)
<=> 16cos2x – 30sinx.cosx = 0 <=> 2cosx(8cosx – 15sinx) = 0
.PNG)
Điều kiện: sinx ≠ 0 <=> x ≠ kπ (k ∈ Z)
(1)<=> 2sin2x + 3cosx=0 <=>2(1-cos2x) + 3cosx=0
<=>2cos2x – 3cosx – 2 = 0 (2)
Đặt cos x = t với điều kiện – 1 ≤ t ≤ 1


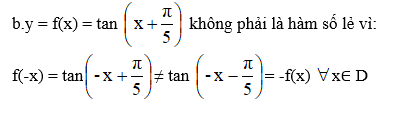
.PNG)
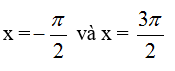
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
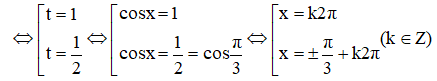
.PNG)


