Bài 1 (trang 36 SGK Đại số 11): Giải phương trình: sin2x – sin x = 0
Lời giải:
sin2x – sin x = 0 => sin x( sin x – 1) = 0
Bài 2 (trang 36 SGK Đại số 11): Giải các phương trình sau:
Lời giải:
a. 2cos2x – 3cosx + 1 =0 (1)
đặt t = cos x, điều kiện – 1 ≤t ≤ 1
(1) 2t2 – 3t + 1 =0
.PNG)
.PNG)
.PNG)
t2 + 2t – 3 = 0 => t1 = -3 (loại), t2 = 1 (nhận)
Với t2 = 1 ta có:
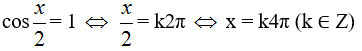
b.8cos2x + 2sinx – 7 = 0 (1)
vì cos2x = 1 – sin2x nên (1)<=>8(1-sin2x) + 2sinx – 7 = 0
<=> 8sin2x – 2sinx – 1 = 0
Đặt t = sin x với điều kiện -1 ≤ t ≤ 1, ta có:
.PNG)
c. 2tan2x + 3tanx + 1 = 0 (3)
Đặt t = tanx, t ∈ R, ta có:
d. tanx – 2cotx + 1 = 0
<=>tan2x + tanx – 2 =0 (với tanx ≠ 0)
Đặt t = tanx, t ∈ R, ta có:
t2 + t – 2 = 0=> t1 = – 2, t2 = 1
Bài 4 (trang 37 SGK Đại số 11): Giải các phương trình sau:
a. 2sin2 x + sinx.cosx – 3cos2 x = 0
b. 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
c. sin2 x + sin2x – 2 cos2 x = 1/2
Lời giải:
a. 2 sin2x + sinx.cosx – 3cos2x = 0 (1)
nhận xét: nếu cosx = 0 thì x = π/2 + kπ không là nghiệm của phương trình (1).
Vậy chia 2 vế cho cos2x (cos2x ≠ 0)
Khi đó (1) <=> 2tan2x + tanx – 3 = 0 (2)
Đặt t = tanx, t ∈ R. Ta có:
(2)<=>2t2 + t – 3 = 0
b.3sin2x – 4sinx.cosx + 5cos2x = 2
<=> 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x )
<=>sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
*Nhận xét: cosx = 0<=>x = π/2 + kπ không là nghiệm của phương trình (1).
Chia hai vế phương trình cho cos2x ( cos2x ≠ 0)
(1) <=> tan2x – 4tanx + 3 = 0 (2)
Đặt t = tan x, t ∈ R, ta có:
(2) <=> t2 – 4t + 3 = 0
*Nhận xét: cosx = 0<=>x = π/2 + kπ không là nghiệm của phương trình (1). Chia 2 vế của phương trình cho cos2x (cos2x ≠ 0). Ta có:
(1)<=>tan2x + 4tanx – 5 = 0 (2)
Đặt t = tan x, khi đó:
(2)<=>t2 + 4t – 5 = 0
Bài 5: (Trang 37 SGK Giải tích lớp 11)
Giải các phương trình sau:
a) cosx – √3sinx = √2 b) 3sin3x – 4cos3x = 5
c) 2sin2x + 2cos2x – √2 = 0 d) 5cos2x + 12sin2x – 13 = 0
Đáp án và hướng dẫn giải bài 5:
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2
⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3
⇔ cos(x +π/3) = √2/2
⇔
b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π
⇔ x = π/6 + α/3 + k(2π/3), k ∈ Z (trong đó α = arccos3/5).
c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2
⇔
d) 5cos2x + 12sin2x – 13 = 0 ⇔ 15/3cosx + 12/13sinx = 1
Đặt α = arccos5/13 thì phương trình trở thành
cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1
⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
Bài 6: (Trang 37 SGK Giải tích lớp 11)
a. tan(2x + 1) tan(3x – 1) = 1
b. tanx + tan(x + π/4) = 1
Đáp án và hướng dẫn giải bài 6:
a. tan(2x + 1) tan(3x – 1) = 1
⇔ tan(2x + 1) = 1/tan(3x – 1) = cot(3x – 1)
Vì tan(3x – 1) cot(3x – 1) = 1
⇔ tan(2x + 1) = tan(π/2 – 3x + 1)
⇔ 2x + 1 = π/2 – 3x + 1 + kπ ⇔ x = π/10 + kπ/5 (k ∈ Z)
b. tanx + tan(x + π/2) = 1 ⇔ tan +


.PNG)
.PNG)
.PNG)

.PNG)
.PNG)







