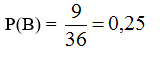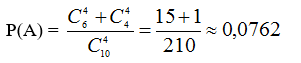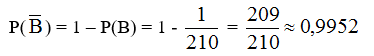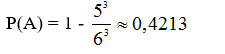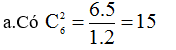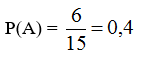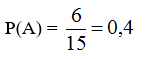Bài 1 (trang 76 SGK Đại số 11): Phát biểu quy tắc cộng
Lời giải:
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.
Quy tắc cộng thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau.
Nếu tập hợp hữu hạn A có n(A) phần tử, tập hợp hữu hạn B có n(B) phần tử, A và B không giao nhau thì số phần tử A ∪ B là:
n (A ∪ B) = n(A) + n(B)
Bài 2 (trang 76 SGK Đại số 11): Phát biểu quy tắc nhân:
Lời giải:
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện thì công việc đó được hoàn thành bởi m.n cách thực hiện.
Quy tắc nhân có thể mở rộng đối với nhiều hành động liên tiếp.
Bài 3 (trang 76 SGK Đại số 11): Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phần tử và một tổ hợp chập k của n phần tử.
Lời giải:
Chỉnh hợp chập k của n phần tử là một tập hợp con k phần tử của một tập hợp phần tử được sắp xếp theo một thứ tự nào đó.
Tổ hợp chập k của n phần tử là tập hợp con k phần tử của một tập hợp n phần tử không để ý đến thứ tự các phần tử của tập hợp con đó. Như vậy với một tổ hợp chập k của n phần tử tạo thành k! chỉnh hợp chập k của n phần tử.
Bài 4 (trang 76 SGK Đại số 11): Có bao nhiêu số chẵn có bốn số được tạo thành từ các chữ số 0, 1, 2, 3, 4, 5, 6 sao cho:
a) Các chữ số có thể giống nhau
b) Các chữ số khác nhau
Lời giải:
a.* Nếu số chẵn có chữ số hàng đơn vị là 0 thì có 6 cách chọn chữ số hàng nghìn, 7 cách chọn chữu số hằng trăm và 7 cách chọn chữ số hàng chục.
vậy số các số chẵn có 4 chữ số tận cùng bằng 0 tạo từ 7 chữ số trên là:
n1 = 6 × 72 = 294 số
*Xét số chẵn ở hàng đơn vị khác 0
– có 3 cách chọn chữ số hàng đơn vị, 6 cách chọn chữ số hàng nghìn, 7 cách chọn chữ số hàng trăm, 7 cách chọn chữ số hàng chục. Số các số chẵn có 4 chữ số với chữ số hàng đơn vị khác 0 tạo thành từ 7 chữ số trên là:
n2 = 3 × 72 = 882 số
Số các số chẵn có 4 chữ số tạo thành từ 7 chữ số trên là:
n = n1 + n2 = 294 + 882 = 1176 số.
b.Số các số chẵn 4 chữ số khác nhau có chữ số hàng đơn vị bằng 0 tạo thành từ 7 chữ số trên là:
n1 = 5 × 6 × 4 = 120 số
Số các số chẵn có 4 chữ số khác nhau tận cùng bằng số khác 0 là:
n2 = 3 ×5 × 5 × 4 = 300 số
vậy số n = n1 + n2 = 120 + 300 = 420 số có 4 chữ số khác nhau tại từ 7 chữ số trên.
Bài 5 (trang 76 SGK Đại số 11): Xếp ngẫu nhiên ba bạn nam và ba bạn nữ ngồi thành sáu ghế kê theo hàng ngang. Tìm xác suất cho:
a. Nam, nữ ngồi xen kẽ nhau.
b. Ba bạn nam ngồi bên cạnh nhau.
Lời giải:
a.Số cách xếp 6 bạn ngồi hàng ngang một cách tùy ý:
n(Ω) = 6! = 720 (cách)
Số cách xếp để nam nữ ngồi xen kẽ là:
n(A) = 2. (3!)2 = 12
Xác suất để các bạn nữ ngồi xen kẽ là:
b.Coi 3 bạn nam như một người thì cách xếp để 3 bạn nam ngồi cạnh nhau như là xếp 4 người trên 4 chỗ và có 3! Cách xếp ba bạn nam trong chỗ chung. Vậy có n(B) = 3!4! cách xếp 3 bạn nam ngồi cạnh nhau.
Xác suất để ba bạn nam ngồi cạnh nhau là:
Bài 6 (trang 76 SGK Đại số 11): Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:
a. Bốn quả lấy ra cùng màu;
b. Có ít nhất một quả cùng màu.
Lời giải:
Xác suất để lấy ra 4 quả cầu cùng màu là:
b. Biến cố đối của biến cố lấy 4 qủa có ít nhất quả cầu trắng là biến cố lấy 4 quả cầu đều đen.
P(B) = 1/210
Xác suất để 4 quả cầu lấy ra có ít nhất một quả cầu trắng là:
Bài 7 (trang 77 SGK Đại số 11): Gieo một con súc sắc ba lần. Tính xác suất sao cho mặt sáu chấm xuất hiện ít nhất một lần
Lời giải:
Biến cố đối với biến cố gieo súc sắc ba lần có ít nhất một lần xuất hiện mặt 6 chấm là biến cố của ba lần đều không xuất hiện mặt 6. Số trường hợp như vậy là: 53 = 125
Xác suất để ba lần gieo có ít nhất một lần xuất hiện mặt sáu chấm là:
Bài 8 (trang 77 SGK Đại số 11): Cho một lục giác đều ABCDEF. Viết các chữ cái A, B, C, D, E, F vào sáu cái thẻ. Lấy ngẫu nhiên hai thẻ. Tìm xác suất sao cho đoạn thẳng mà các đầu mút là các điểm được ghi trên hai thẻ đó là:
a. Cạnh của lục giác.
b. Đường chéo của lục giác.
c. Đường chéo nối hai đỉnh đối diện của lục giác.
Lời giải:
cách lấy 2 tấm thẻ ghi 2 điểm trong 6 điểm. Có 6 trường hợp chọn được hai tấm thẻ ghi hai đỉnh kề nhau tạo thành một cạnh của lục giác.
Xác suất để lấy hai thẻ ghi hai điểm là một cạnh của lục giác là:
b. Xác suất để lấy hai thẻ ghi hai điểm là hai mút của đường chéo là:
P(B) = 1- P(A) = 1 – 0,4 = 0, 6
c. Xác suất để lấy hai thẻ ghi hai đỉnh đối diện của lục giác:
P(C) = 3/15 = 0,2
Bài 9 (trang 77 SGK Đại số 11): Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:
a. Hai con súc sắc đều xuất hiện mặt chẵn.
b. Tính các số chấm trên hai con súc sắc là số lẻ.
Lời giải:
a.Xác suất để hai con súc sắc xuất hiện mặt chẵn là:
b.Xác suất để tính số chấm trên hai con súc sắc là số lẻ: