Top 20 nguyên hàm của 2x chính xác nhất

1. Nguyên hàm là gì?

Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.

2. Tính chất nguyên hàm

Nguyên hàm có 3 tính chất quan trọng cần nhớ:

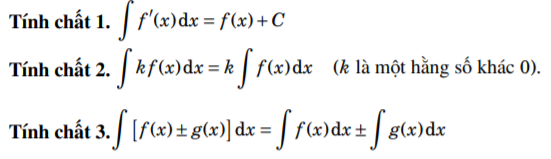
2. Bảng nguyên hàm

a) Bảng công thức nguyên hàm cơ bản

b) Bảng nguyên hàm mở rộng

3. Các phương pháp tính nguyên hàm

Dạng 1. Nguyên hàm cơ bản

Dạng 2. Sử dụng phương pháp ĐỔI BIẾN để tìm nguyên hàm

a) Đổi biến tổng quát

• Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
• Bước 2: Tính vi phân hai về dt = φ'(x)dx
• Bước 3: Biểu thị f(x)dx = g[φ(x)]φ'(x)dx = g(t)dt.
• Bước 4: Khi đó $I = int {fleft( x right)dx} $ $ = int {gleft( t right)dt} $ $ = Gleft( t right) + C$

Ví dụ: Tìm nguyên hàm của hàm số $I = int {frac{1}{{xsqrt {ln x + 1} }}dx} $

Hướng dẫn giải

• Bước 1: Chọn $t = sqrt {ln x + 1} Rightarrow {t^2} = ln x + 1$
• Bước 2: Tính vi phân hai về dt = – 3sinx.dx
• Bước 3: Biểu thị $int {fleft( x right)dx} = – frac{1}{3}int {frac{1}{t}.dt} $
• Bước 4: Khi đó $I = – frac{1}{3}ln left| t right| + C$ $ = – frac{1}{3}ln left| {1 + 3cos x} right| + C$

b) Đổi biến dạng 1

c) Đổi biến dạng 2

Dạng 3. Nguyên hàm từng phần

Nguyên tắc chung để đặt u và dv: Tìm được v dễ dàng và ∫v.du tính được

Nhấn mạnh: Thứ tự ưu tiên khi chọn đặt u: “Nhất lô, nhì đa, tam lượng, tứ mũ” (hàm lôgarit, hàm đa thức, hàm lượng giác, hàm mũ).

Xem thêm: Tổng hợp 9 25 mod 10 div 2 hay nhất

Ví dụ: Tìm nguyên hàm của hàm số f(x) = x.e2x

Hướng dẫn giải

Bước 1: Đặt $left{ begin{array}{l} u = ln left( {2x} right)\ dv = x.dx end{array} right. Rightarrow left{ begin{array}{l} du = frac{1}{x}\ v = frac{{{x^2}}}{2} end{array} right.$

Bước 2: Ta thấy $Fleft( x right) = int {fleft( x right)} dx$ $ = frac{{{x^2}}}{2}.ln left( {2x} right) – int {frac{1}{x}.frac{{{x^2}}}{2}} dx$ $ = frac{{{x^2}}}{2}.ln left( {2x} right) – frac{{{x^2}}}{4} + C$ $ = frac{{{x^2}}}{2}.left( {ln left( {2x} right) – frac{1}{2}} right) + C$

Dạng 4. cách tính nguyên hàm bằng máy tính

Cho nguyên hàm $int {fleft( x right)dx} $ = F(x) + C. Hãy tìm f(x) hoặc F(x)

Hướng dẫn

Để giải, mình sẽ hướng dẫn cách bấm máy tính nguyên hàm nhanh theo 3 bước sau:

Bước 1: Nhấn shift $frac{d}{{dx}}left( {Fleft( x right)} right){|_{x = X}} – fleft( X right)$

Bước 2: Nhấn phím Calc nhập X = 2.5

Bước 3: Đánh giá nghiệm

• Nếu kết quả bằng 0 (gần bằng 0 ) thì đó là đáp án cần chọn

Ví dụ: Tìm tất cả nghiệm của hàm số f(x) = $frac{1}{{2x + 3}}$ là

A. $frac{1}{2}.lnleft| {2x + 3} right| + C$

Xem thêm: Top 15 i should like someone to take me out to dinner

B. $frac{1}{2}.lnleft( {2x + 3} right) + C$

C. ln|2x + 3| + C

D. $frac{1}{{ln 2}}.$ln|2x + 3| + C

Hướng dẫn bấm máy tính

Bước 1: Nhập vào máy tính casio $frac{d}{{dx}}left( {frac{1}{2}.ln left( {left| {2x + 3} right|} right)} right){|_{x = X}} – frac{1}{{2x + 3}}$

Bước 2: CALC X = -2

Lưu ý: Trong kết quả A và C nếu cho X = 2 thì đều cho kết quả là 0. Vậy khi có trị tuyệt đối thì cho X một giá trị cho biểu thức trong trị tuyệt đối âm.

Kết luận: Chọn đáp án A.

Dạng 5. Tính nguyên hàm của hàm số

Tìm nguyên hàm dạng $left[ begin{array}{l} I = int {P(x)sin axdx} \ I = int {P(x)c{rm{osaxdx}}} end{array} right.$ với $P(x)$ là một đa thứcTa lựa chọn một trong hai cách sau:

Cách 1: Sử dụng nguyên hàm từng phần, thực hiện theo các bước sau:

• Bước 1: Đặt: $left{ begin{array}{l} u = P(x)\ dv = left[ begin{array}{l} {mathop{rm s}nolimits} {rm{inaxdx}}\ {rm{cosaxdx}} end{array} right. end{array} right.$ $ to left{ begin{array}{l} du = P'(x)dx\ v = left[ begin{array}{l} frac{{ – 1}}{a}c{rm{osax}}\ frac{{rm{1}}}{{rm{a}}}sin ax end{array} right. end{array} right.$
• Bước 2: Thay vào công thức nguyên hàm từng phần.
• Bước 3: Tiếp tục thủ tục như trên ta sẽ khử được bậc của đa thức.

* Cách 2: Sử dụng phương pháp hệ số bất định, thực hiện theo các bước sau:

• Bước 1: Ta có: $I = int {P(x)c{rm{osaxdx}}} $ ${{rm{ = A(x)sinax + B(x)cosax + C}}}$ $(1)$, trong đó $A(x)$ và $B(x)$ là các đa thức cùng bậc với $P(x).$
• Bước 2: Lấy đạo hàm hai vế của $(1)$: $P(x)c{rm{osax}}$ ${rm{ = A'(x)cosax – A(x)a}}{rm{.sinax}}$ ${rm{ + B'(x)sinax + aB(x)cosax}}.$
• Bước 3: Sử dụng phương pháp hệ số bất định ta xác định được $A(x)$ và $B(x).$

Nhận xét: Nếu bậc của đa thức lớn hơn $3$ thì cách 1 tỏ ra cồng kềnh, vì khi đó ta thực hiện số lần nguyên hàm từng phần bằng với số bậc của đa thức, cho nên ta đi đến nhận định như sau:

• Nếu bậc của đa thức nhỏ hơn hoặc bằng $2$: Ta sử dụng cách 1.
• Nếu bậc của đa thức lớn hơn hoặc bằng $3$: Ta sử dụng cách 2.

Xem thêm: Top 19 thung lũng sông hồng ở nước ta được hình thành

Ví dụ: Tìm nguyên hàm $int {x{{sin }^2}xdx} .$

Giải

Ta có: $I = int {xleft( {frac{{1 – c{rm{os2x}}}}{2}} right)dx} $ ${ = frac{1}{2}int {xdx} – frac{1}{2}int {xcos 2xdx} }$ ${ = frac{1}{4}{x^2} – frac{1}{2}J}$ $(1).$

Tính: $J = int {xcos 2xdx} .$

Đặt: $left{ begin{array}{l} u = x\ dv = c{rm{os2xdx}} end{array} right.$ $ to left{ begin{array}{l} du = dx\ v = frac{1}{2}sin 2x end{array} right.$ $ Rightarrow J = frac{x}{2}sin 2x – frac{1}{2}int {sin 2xdx} $ ${ = frac{x}{2}sin 2x + frac{1}{4}c{rm{os2x + C}}}.$

Thay vào $(1)$: $I = frac{1}{4}{x^2} – frac{1}{2}left( {frac{x}{2}sin 2x + frac{1}{4}c{rm{os2x}}} right)$ $ = frac{1}{4}left( {{x^2} – xsin 2x – frac{1}{2}c{rm{os2x}}} right) + C.$

3. Bài tập nguyên hàm

Bài tập 2: Tìm nguyên hàm $I = int {left( {{x^3} – {x^2} + 2x – 3} right){mathop{rm s}nolimits} {rm{inx}}dx} .$

Giải

Theo nhận xét trên, ta sử dụng phương pháp hệ số bất định. Ta có: $I = int {left( {{x^3} – {x^2} + 2x – 3} right){mathop{rm s}nolimits} {rm{inx}}dx} $ $ = left( {{a_1}{x^3} + {b_1}{x^2} + {c_1}x + {d_1}} right)c{rm{osx}}$ ${rm{ + }}left( {{a_2}{x^3} + {b_2}{x^2} + {c_2}x + {d_2}} right){mathop{rm s}nolimits} {rm{inx}}$ $(1).$

Lấy đạo hàm hai vế của $(1)$:

$ Leftrightarrow left( {{x^3} – {x^2} + 2x – 3} right){mathop{rm s}nolimits} {rm{inx}}$ ${rm{ = [}}{{rm{a}}_{rm{2}}}{x^3} + left( {3{a_1} + {b_2}} right){x^2}$ $ + left( {2{b_1} + {c_2}} right)x + {c_1} + {d_2}{rm{]cosx}}$ $ – [{{rm{a}}_{rm{1}}}{x^3} – left( {3{a_2} – {b_1}} right){x^2}$ $ – left( {2{b_2} – {c_1}} right)x + {c_2} – {d_1}]sin x$ $(2).$

Đồng nhất thức ta được: $left{ begin{array}{l} {a_2} = 0\ 3{a_1} + {b_2} = 0\ 2{b_1} + {c_2} = 0\ {c_1} + {d_2} = 0 end{array} right.$ và $left{ begin{array}{l} – {a_1} = 1\ 3{a_2} – {b_1} = – 1\ 2{b_2} – {c_1} = 2\ – {c_2} + {d_1} = – 3 end{array} right.$ $ Rightarrow left{ begin{array}{l} {a_1} = – 1;{a_2} = 0\ {b_1} = 1;{b_2} = 3\ {c_1} = 4;{c_2} = – 2\ {d_1} = 1;{d_2} = – 4 end{array} right.$

Khi đó: $I = left( { – {x^3} + {x^2} + 4x + 1} right)c{rm{osx}}$ ${rm{ + }}left( {{rm{3}}{{rm{x}}^{rm{2}}} – 2x + 4} right){mathop{rm s}nolimits} {rm{inx + C}}.$

Top 20 nguyên hàm của 2x tổng hợp bởi Lambaitap.edu.vn

Xem thêm: Top 9 bài 34 trang 94 sgk toán 7 tập 1

Xem thêm: Top 8 soạn bài vịnh khoa thi hương

Xem thêm: Top 27 bài 43 trang 23 sgk toán 7 tập 1 đầy đủ nhất