Bài 1 (trang 17 SGK Đại số 11): Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Lời giải:
a. y = tan x nhận giá trị bằng 0
=> tan x = 0
x = – π => tan (- π) = 0 (thỏa)
x = 0=>tan (0) = 0 (thỏa)
x = π =>tan ( π = 0 (thỏa)
Vậy x nhận các giá trị { – π; 0; π}
b. y = tan x nhận giá trị bằng 1.
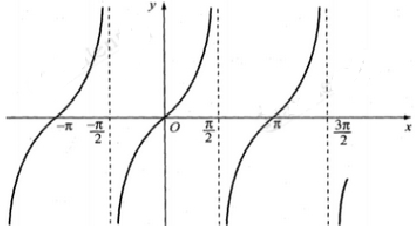
c. Hàm số y = tan x tuần hoàn với chu kì π
Đồ thị hàm số y = tan x:
– dựa vào đồ thị ta thấy trên đoạn [- π ; – 3π/2] , hàm số y = tan x nhận giá trị dương trên các khoảng
d. Từ đồ thị trên, hàm số y = tan x nhận giá trị âm khi trên các khoảng:
Bài 2 (trang 17 SGK Đại số 11): Tìm tập xác định của hàm số:
Lời giải:
Tập xác định D = R {x|sin x = 0 } = R {kπ, k ∈ Z}.
.PNG)
=> Tập xác định D = R {k2π, k ∈ Z}
.PNG)
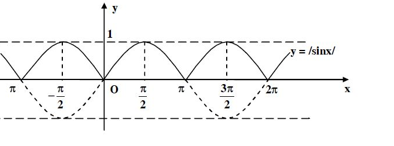
Bài 3 (trang 17 SGK Đại số 11): Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = | sin x|
Lời giải:
Hàm số y = sin x có chu kì 2π
Đồ thị:
Từ đồ thị hàm số y = sin x ta lấy đối xứng qua trục Ox các phần đồ thị trên đoạn
[π+k2π; 2π+k2π], giữ nguyên phần đồ thị còn lại (k ∈ Z), thì đó chính là đồ thị hàm số y = |sin x|
Bài 4 (trang 17 SGK Đại số 11): Chứng minh rằng sin 2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x
Lời giải:
Ta có: sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)
Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
Đồ thị:
Bài 5 (trang 18 SGK Đại số 11): Dựa vào đồ thị hàm số y = cos x, tìm các giá trị của x để cos x = 1/2
Lời giải:
Đồ thị hàm số y = cos x:
Dựa vào đồ thị hàm số y = cos x:
Để cos x = 1/2 thì đường thẳng y = 1/2 cắt đồ thị hàm số y = cos x, hoành độ giao điểm giữa y = cos x và y = 1/2 là
Bài 6 (trang 18 SGK Đại số 11): Dựa trên đồ thị hàm số y = sin x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.
Lời giải:
Đồ thị hàm số y = sin x:
Dựa vào đồ thị hàm số y = sin x, để hàm số nhận giá trị dương thì:
x ∈ (-2π; -π); (0; π); (2π; 3π)…
hay x ∈ (k2π; π + k2π) với k ∈ R.
Bài 7 (trang 18 SGK Đại số 11): Dựa vào đồ thị hàm số y = cos x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm.
Lời giải:
Đồ thị hàm số y = cos x:
Dựa vào đồ thị hàm số y = cos x, để hàm số nhận giá trị âm thì:
Bài 8 (trang 18 SGK Đại số 11): Tìm giá trị lớn nhất của các hàm số:
Lời giải:
b. y = 3 – 2sin x
Ta có: – 1 ≤ sin x ≤ 1
<=> – 2 ≤ 2sin x ≤ 2 <=>2 ≥ 2sin x ≥- 2
<=>5 ≥ 3 – 2sin x ≥ 1<=>1 ≤ y ≤ 5
=>ymax = 5<=> sin x = -1
<=>x = -π/2 + k2π (k ∈ Z)


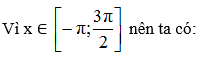
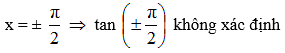
.PNG)
.PNG)
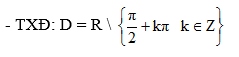
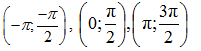
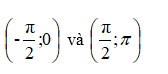
.PNG)
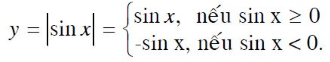
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)


