Top 20+ cho biểu thức p đầy đủ nhất

1. Căn bậc hai

a. Khái niệm: Căn bậc hai của một số a không âm là số x sao cho x2=a.

b. Tính chất:

– Số âm không có căn bậc hai.

– Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết 0=0.

– Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là a, số âm ký hiệu là -a.

2. Căn bậc hai số học

a. Định nghĩa: Với số dương a, số a được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.

Chú ý. Với a ≥ 0, ta có:

Nếu thì x ≥ 0 và x2=a;

Nếu x ≥ 0 và x2= a thì x=a.

– Ta viết x=a⇔x≥0x2=a.

b. Phép khai phương:

– Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).

– Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.

3. So sánh các căn bậc hai số học

Định lí. Với hai số a và b không âm, ta có: a<b⇔a<b.

4. Căn thức bậc hai

Với A là một biểu thức đại số, người ta gọi A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

A xác định (có nghĩa) khi A lấy giá trị không âm.

5. Hằng đẳng thức A2=|A|

Định lí. Với mọi số a, ta có a2=|a|.

Chú ý. Một cách tổng quát, với A là một biểu thức ta có A2=|A|, có nghĩa là:

Xem thêm: Top 15 bài 6 công nghiệp hóa hiện đại hóa đất nước

A2=A nếu A ≥ 0 (tức là A lấy giá trị không âm);

A2=-A nếu A < 0 (tức là A lấy giá trị âm).

6. Căn bậc hai của một tích

Định lí. Với hai số a và b không âm, ta có a . b=a . b.

Chú ý: Định lí trên có thể mở rộng cho tích của nhiều số không âm.

7. Quy tắc khai phương một tích

Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả lại với nhau.

a . b=a . b (với a, b ≥ 0).

8. Quy tắc nhân các căn bậc hai

Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới căn với nhau rồi khai phương kết quả đó.

a . b=a . b (với a, b ≥ 0).

Chú ý. Một cách tổng quát, với hai biểu thức A và B không âm ta có:

A  .  B=A  .  B.

Đặc biệt, với biểu thức A không âm ta có:

(A)2=A2=A.

9. Căn bậc hai của một thương

Định lí. Với số a không âm và số b dương, ta có: ab=ab.

10. Quy tắc khai phương một thương

Muốn khai phương một thương ab, trong đó số a không âm và số b dương, ta có thể lần lượt khai phương của các số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.

ab=ab (với a ≥ 0, b > 0).

11. Quy tắc chia hai căn bậc hai

Muốn chia hai căn bậc hai của số a không âm và số b dương, ta có thể lấy số a chia cho số b rồi khai phương kết quả vừa tìm được.

ab=ab (với a ≥ 0, b > 0).

Chú ý. Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có:

Xem thêm: Top 20+ văn 11 trang 116

AB=AB.

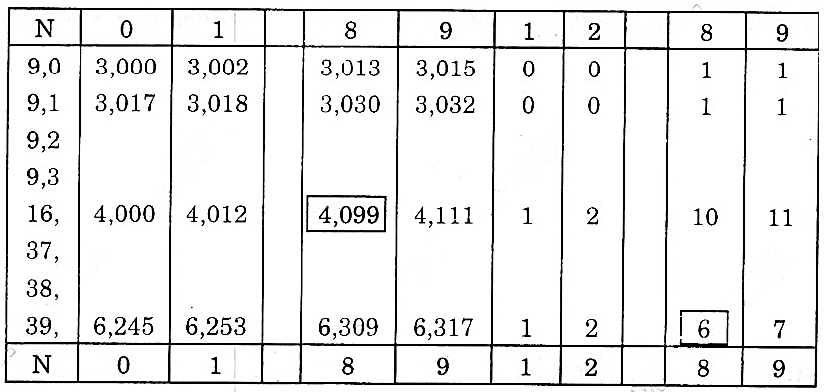
12. Giới thiệu bảng căn bậc hai

+ Bảng được chia thành các hàng và các cột.

+ Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.

+ Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.

+ Bảng căn bậc hai.

13. Đưa một thừa số ra ngoài dấu căn

• Với a ≥ 0, b ≥ 0, ta có: a2b=ab. Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.

• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.

• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.

Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có A2 . B=  |A|B, tức là:

Nếu A ≥ 0 và B ≥ 0 thì A2B=AB;

Nếu A < 0 và B ≥ 0 thì A2B=−AB.

14. Đưa thừa số vào trong dấu căn

• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.

Với A ≥ 0 và B ≥ 0 thì AB=A2B.

Với A < 0 và B ≥ 0 thì AB=− A2B.

• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.

15. Khử mẫu của biểu thức lấy căn

Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:

AB=AB|B|.

16. Trục căn thức ở mẫu

Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.

Xem thêm: Top 9 hình đa diện nào không có tâm đối xứng

Tổng quát:

• Với các biểu thức A, B mà B > 0 ta có:

AB=ABB.

• Với các biểu thức A, B, C mà A ≥ 0, A≠B2, ta có:

CA±B=C(A∓B)A−B2.

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:

CA±B=C(A∓B)A−B.

17. Rút gọn biểu thức chứa căn thức bậc hai

– Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.

– Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ.

18. Khái niệm căn bậc ba

Định nghĩa: Căn bậc ba của một số thực a là số x sao cho x3=a.

• Mỗi số a đều có duy nhất một căn bậc ba.

• Căn bậc ba của một số a được kí hiệu là x=a3 (số 3 gọi là chỉ số căn).

• Phép lấy căn bậc ba của một số gọi là phép khai căn bậc ba.

Chú ý. Từ định nghĩa căn bậc ba, ta có (a3)3=a33=a.

Nhận xét:

– Căn bậc ba của số dương là số dương;

– Căn bậc ba của số âm là số âm;

– Căn bậc ba của số 0 là số 0.

19. Tính chất căn bậc ba

• a < b ⇔a3<b3 .

• ab3=a3 .  b3.

• Với b ≠ 0, ta có: ab3=a3b3.

Top 20 cho biểu thức p tổng hợp bởi Lambaitap.edu.vn

Xem thêm: Top 10+ nhận định nào dưới đây là chưa chính xác

Xem thêm: Top 13 vở bài tập toán lớp 2 tập 1 trang 34

Xem thêm: Top 10+ a 4 b 4 c 4 đầy đủ nhất