Bài 1 (trang 77 SGK Hình học 11): Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.
a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).
b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).
c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
Lời giải:
a) Giao tuyến của các cặp mặt phẳng
*Giao tuyến của (AEC) và (BFD)
• Trong hình thang ABCD, AC cắt DB tại G, ta có:
Tương tự, AE cắt BF tại H,
Ta có H
Vậy GH = (AEC) ∩ (BFD)
*Giao tuyến của (BCE) và (ADF)
Trong hình thang ABCD, BC cắt AD tại I, ta có: I ∈ (BCE) ∩ (ADF)
Trong hình thang ABEF, BE cắt AF tại K, ta có: K ∈ (BCE) ∩ (ADF)
Vậy IK = (BCE) ∩ (ADF)
b) Giao điểm của AM với mp(BCE)
*Trong mp(ADF), AM cắt PQ tại N, ta có:
N ∈AM
N ∈ PQ (BCE) N ∈ (BCE)
Vậy N = AM ∩ (BCE)
c) Chứng minh AC và BF không cắt nhau
*Giả sử AC và BF cắt nhau tại R, ta có :
=> AC, BF, AB đồng qui tại R :vô lí !
Vậy AC và BF không cắt nhau.
Bài 2 (trang 77 SGK Hình học 11): Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của đoạn thẳng SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, hãy tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).
Lời giải:
a) Tìm tiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = ME ∩ SD và trong mp(SAB), gọi R = MF ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Các đoạn giao tuyến này khép kín tạo thành thiết diện là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN Trong (SBD), SO ∩ MH = I
Vậy H = SO ∩ (MNP)
Bài 3 (trang 77 SGK Hình học 11): Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giap điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
Lời giải:
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
Do đó E ∈ (SAD) ∩ (SBC). Mà S ∈ (SAD) ∩ (SBC). Nên SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
Trong mp(SBE), gọi F = MN ∩ SE => (AMN) = (AMF)
Trong mp(SAE), AF ∩ SD = P
c) Tìm thiết diện với mp(AMN):
Mặt phẳng (AMN) cắt các mặt bên của hình chóp S.ABCD theo các đoạn giao tuyến AM, MN, NP, PA.
Bài 4 (trang 78 SGK Hình học 11): Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.
a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)
b) Gọi I = AC ∩ BD, J = A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.
c) Cho AA’ = a, BB’ = b, CC’ = c. Hãy tính DD’.
Lời giải:
a) ABDC là hình bình hành, nên:
AB // DC (1)
Theo giả thiết Ax // Dt (2)
Từ (1) và (2) suy ra đpcm.
b) Do (Ax, By) // (Cz, Dt) nên các giao tuyến A’D’ và B’C’ của các mặt phẳng này giao với (β) song song với nhau, A’B’ // D’C’.
Chứng minh tương tự, ta có: A’D’ // B’C’
Suy ra tứ giác A’B’C’D’ là hình bình hành, cho ta J là trung điểm của A’C’. Ax // Cz nên tứ giác ACC’A’ là hình thang, I, J theo thứ tự lần lượt là các trung điểm của các cạnh bên AC và A’C’ nên IJ // AA’.
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’ DD’ = a + c – b


.PNG)
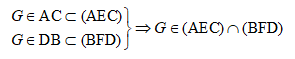
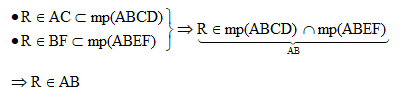
.PNG)
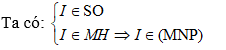
.PNG)
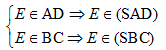
.PNG)


