Bài 1 (trang 157 SGK Đại số 11): Tìm số gia của hàm số f(x) = x3, biết rằng:
a.x0 = 1; Δx = 1;
b.x0 = 1; Δx = -0,1;
Lời giải:
Số gia của hàm số được tính theo công thức:
Δy = f(x) – f(x0) = f(x0 + Δx) – f(x0)
a. Δy = f(1 + 1) – f(1) = f(2) – f(1) = 23 – 13 = 7
b. Δy = f(1 – 0,1) – f(1) = f(0,9) – f(1) = (0,9)3 – 13 = -0,271.
Bài 2 (trang 156 SGK Đại số 11):
Lời giải:
Bài 3 (trang 156 SGK Đại số 11): Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:
Lời giải:
y = x2 +x tại x0=1
*Giả sử Δx là số gia của đối số tại x0 = 1. Ta có:
Δy = f(x0+Δx) – f(x0 ) = f(1 – Δx) = f(1)
= (1 + Δx)2 + (1 + Δx)-(12 + 1)
= Δx(3 + Δx)
* Δx/Δy = 3 + x
* limΔx/Δy = lim(3 – Δx) = 3(vớiΔx →0)
Bài 4 (trang 156 SGK Đại số 11): Chứng minh rằng hàm số:
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.
Lời giải:
.PNG)
Bài 5 (trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến đường cong y=x^3.
a. Tại điểm (-1; -1);
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Lời giải:
Bài 6 (trang 156 SGK Đại số 11): Viết phương trình tiếp tuyến của hypebol y = 1/x
Lời giải:
Bài 7 (trang 157 SGK Đại số 11): Một vật rơi tự do theo phương trình s=1/2 gt2, trong đó g≈9,8m/s2 là gia tốc trọng trường.
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t+Δt, trong các trường hợp Δt=0,1s; Δt=0,05s; Δt=0,001s.
b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
Lời giải:




.PNG)
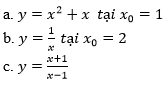
.PNG)
.PNG)

.PNG)
.PNG)


