Bài 1 (trang 159 SGK Đại số 10):
.PNG)
.PNG)
b) B = {x ∈ R| 4 < x ≤ 5} = (4; 5].
A B = [3; 4]
R (A B) = R [3; 4] = (-∞; 3) ∪ (4; +∞)
Bài 2 (trang 160 SGK Đại số 10): Cho phương trình : mx2 – 2x – 4m – 1 = 0
a. Chứng mình rằng với mọi giá trị của m ≠ 0 phương trình đã cho có hai nghiệm phân biệt.
b. Tìm giá trị của m để -1 là một nghiệm của phương trình. Sau đó tìm nghiệm còn lại.
Lời giải
a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1 = (2m + 1/2)2 + 3/4 > 0 với ∀ m
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.12 – 2.(-1) – 4m – 1 = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.
Bài 3 (trang 160 SGK Đại số 10): Cho phương trình : x2 – 4mx +9(m-1)2
a. Xem xét với các giá trị nào của m thì phương trình trên có nghiệm ?
b. Gỉa sử x1, x2 là nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức giữa x1 và x2 độc lập với m.
c. Xác định giá trị của m để hiệu các nghiệm của phương trình bằng 4.
Lời giải
a) Xét: x2 – 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 – 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
.PNG)
.PNG)
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
Bài 4 (trang 160 SGK Đại số 10): Chứng minh rằng các bất đẳng thức :
Lời giải
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Áp dụng bất đẳng thức Cô-si cho hai số dương và 1 ta có:
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.
Bài 5 (trang 160 SGK Đại số 10): Giải hệ phương trình sau bằng cách đưa về hệ tam giác :
Lời giải
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3) ta được:
.PNG)
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)
Bài 6 (trang 160 SGK Đại số 10):
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Xét sự biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Lời giải
a) f(x) = 2x.(x+2) – (x+2)(x+1) = 2x2 + 4x – (x2 + 3x + 2) = x2 + x – 2
Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.
Vậy:
+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)
+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)
+ f(x) = 0 nếu x = -2 hoặc x = 1.
b)
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:
+ Tập xác định: D = R
+ Đỉnh I1( -1; -2)
+ Trục đối xứng: x = -1
+ Giao điểm với trục tung tại gốc tọa độ.
+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).
+ Bảng biến thiên:
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:
+ Tập xác định D = R.
+ Đỉnh
+ Trục đối xứng: x = -3/2
+ Giao với trục tung tại D(0; 2)
+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)
+ Bảng biến thiên
.PNG)
* Đồ thị:
.PNG)
* Tìm tọa độ giao điểm:
Cách 1: Dựa vào đồ thị hàm số:
Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)
Cách 2: Tính:
Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:
2x(x + 2) = (x + 2)(x + 1)
⇔ (x + 2).2x – (x + 2)(x + 1) = 0
⇔ (x + 2).(2x – x – 1) = 0
⇔ (x + 2).(x – 1) = 0
⇔ x = -2 hoặc x = 1.
+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)
+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).
c)
+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)
⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c
+ Ta có bảng biến thiên của hàm số y = ax2 + 3x + c:
.jpg)
Bài 7 (trang 161 SGK Đại số 10): Chứng minh các hệ thức sau :
Lời giải
Bài 8 (trang 161 SGK Đại số 10): Rút gọn các biểu thức sau :
Lời giải
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)


.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
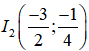
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)


